Sin torsión, Amortiguación de oscilaciones torsionales

Al igual que el daño que causan los soldados que cruzan un puente marcando el paso y efecto del viento en el desventurado puente Tacoma Narrows, la resonancia no amortiguada puede ser perjudicial en los accionamientos eléctricos, la cual puede amplificar los impulsos del par motor a una de las frecuencias propias de la transmisión y causar oscilaciones de torsión y grandes variaciones que acabarán dañando los engranajes y la transmisión
Por Mehmet Mercangöz, Silvia Mastellone, Stefan Almér, Thomas Besselmann, Pieder Jörg, Jouko Niiranen, Luca Peretti y Veli-Matti Leppänen
Hay tres formas de afrontar las vibraciones torsionales: eliminarlas en el diseño, limitar el funcionamiento a un margen de velocidades seguro y confiar en que la inercia del sistema atenúe cualquier excitación, así como controlar y manipular activamente la transmisión para neutralizar las oscilaciones torsionales.
Las transmisiones eléctricas son frecuentes en el mundo moderno; convierten la energía eléctrica a mecánica con muchas aplicaciones industriales y efectúan la conversión inversa en los generadores eléctricos. Todos estos sistemas rotativos de velocidad variable experimentan vibraciones de torsión durante el arranque, la parada y el funcionamiento. En casos problemáticos, las vibraciones torsionales pueden aumentar hasta provocar el desgaste de los engranajes o la rotura de los ejes.
En consecuencia, hay que evaluar las características de respuesta torsional de los equipos rotatorios y sus bucles de control para verificar el funcionamiento estable del sistema. Esto es especialmente importante con potencias nominales altas, porque el diámetro del eje y, por tanto, su resistencia mecánica, no puede aumentarse proporcionalmente a la potencia. Las consecuencias de un fallo mecánico en un accionamiento de gran potencia son bastante graves.
La intensidad de las vibraciones depende de la magnitud de la excitación torsional y de la diferencia entre las frecuencias de excitación y las naturales asociadas con los modos del sistema del eje y su amortiguación. El objetivo es, naturalmente, evitar la coincidencia de ambas frecuencias. Por lo tanto, deben calcularse las frecuencias naturales del sistema y definirse las fuerzas de excitación que se pueden producirse. No es tarea fácil en sistemas complejos con muchos elementos en la transmisión. En ciertos casos, hay que tener en cuenta la rigidez finita de la bancada del motor y otras partes flexibles de las estructuras circundantes.
Una dificultad concreta en el caso de sistemas electromecánicos es que los componentes eléctricos y mecánicos normalmente se diseñan, analizan y controlan por separado, sin tener en cuenta su interacción mutua o con otros componentes. Además, hay casos en los que no se dispone de antemano de información precisa sobre el sistema. La forma de mantener el funcionamiento estable de la transmisión es limitar la incertidumbre, definiendo límites para los parámetros del sistema y teniendo en cuenta el margen de resistencia a todos los regímenes mediante el control adecuado.
Transmisiones
Una transmisión electromecánica tiene tres componentes fundamentales: la red eléctrica, transformadores y filtros de entrada/salida; el convertidor eléctrico y el motor o generador; y la carga o turbina. Todos pueden contribuir a la dinámica torsional. Las variaciones en la red afectan directamente al comportamiento de la transmisión de un motor directo en línea. Un convertidor eléctrico puede aislar en gran medida el sistema torsional de las perturbaciones de la red, pero, por la conmutación con semiconductores, se producen frecuencias de excitación que depende de la velocidad del motor.
Casi todas las máquinas eléctricas de Corriente Alterna (CA) crean un par muy suave con una tensión sinusoidal, pero construcciones especiales como las de imán permanente pueden tener un par dentado importante. Finalmente, la carga mecánica de un motor o de una turbina varía con la aplicación y es, en ciertos casos, difícil de predecir.
Al estudiar las resonancias torsionales de la transmisión, se efectúa en primer lugar el llamado análisis modal y se comparan las frecuencias naturales con las posibles frecuencias de excitación. En estudios más detallados, se modeliza el sistema eléctrico con elementos resistivos, inductivos y capacitivos discretos, y la transmisión mecánica con inercias discretas unidas a elementos elásticos sin inercia que representan ejes y acoplamientos. Como se muestra en las figuras 1 y 2, se verifica y optimiza la respuesta para varias excitaciones con las funciones de transferencia o ecuaciones diferenciales del sistema de control.
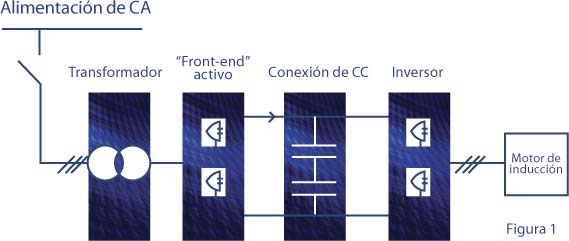
Idealmente, si el modelo cubre todo el desempeño del sistema, se puede diseñar un control en consecuencia para garantizar el comportamiento; pero normalmente sólo se conocen con precisión razonable las grandes inercias concentradas y la elasticidad principal. Las inercias menores y distribuidas, como las de una caja reductora, son más difíciles de evaluar. Los coeficientes de amortiguación son otra fuente de imprecisión, pues es casi imposible obtenerlos para muchos elementos, por lo que suelen desestimarse, aunque una amortiguación fuerte tiene un efecto notable sobre la frecuencia y, en especial, la amplitud de resonancia. Por el contrario, las características eléctricas del motor y de su control no pueden ignorarse en el modelo torsional de la transmisión, ya que modifican sustancialmente las frecuencias naturales y la amplificación de las excitaciones.
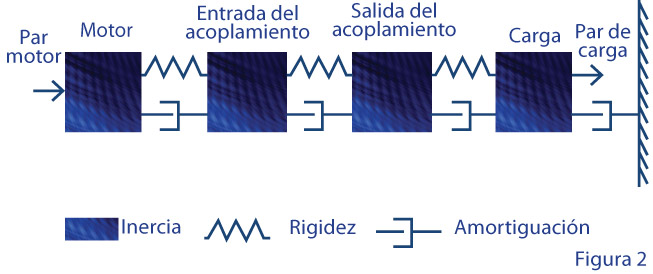
Como los componentes eléctricos y mecánicos de la transmisión están interconectados y las oscilaciones se propagan entre ellos, el análisis no puede limitarse siempre a uno o a otro, sino que debe extenderse desde el eje hasta la red eléctrica, incluyendo cualquier convertidor de frecuencia opcional. Hecho esto, se pueden formular las estrategias para la solución.
Soluciones
Dependiendo de la naturaleza de las vibraciones, pueden aplicarse distintas estrategias para reducirlas, limitarlas o evitarlas. Estas estrategias suelen pertenecer a una de tres categorías: diseño del sistema, funcionamiento del sistema y amortiguación activa.
La estrategia de diseño del sistema adopta medidas contra las vibraciones, incorporando componentes disipadores como acoplamientos amortiguados con elastómero o hidrodinámicos, los cuales reducen la amplitud de la vibración convirtiendo la energía de excitación en calor, o conformando el espectro de excitación con filtros senoidales en la salida del convertidor. Estos métodos se denominan de amortiguación pasiva. Aunque prácticos en algunas aplicaciones, presentan el inconveniente de que la energía disipada se desperdicia y el filtrado mecánico o eléctrico ralentiza la dinámica del sistema. Suelen ser caros y los acoplamientos de elastómero envejecen.
El segundo método emplea el análisis modal para determinar márgenes de velocidad sin resonancia, en los que es posible el funcionamiento continuo. Como el número de polos del motor afecta a esos márgenes, se elige el número que mejor se ajusta a las necesidades del proceso. El método es práctico y sencillo de aplicar. Pero no siempre es posible encontrar márgenes de velocidad suficientemente amplios, y no siempre son aceptables las rápidas aceleraciones y deceleraciones necesarias para cruzar los márgenes de velocidades prohibidos.
La tercera clase de estrategias se basa en la emulación del comportamiento físico de los amortiguadores. Los métodos de amortiguación activa de resistencias virtuales basados en modelos son ejemplos de soluciones activas que ofrece el software. Los métodos de espacio de estados son especialmente útiles para sistemas de orden elevado y modelizan y controlan todo el sistema, incluyendo las interconexiones, y tienen en cuenta todas las variables no lineales, como fricción y retroceso. Por su parte, los métodos basados en la frecuencia son mejores para identificar los modos críticos.
También suelen emplearse métodos híbridos que combinan dos o más de estas estrategias. Así, puede reducirse la rigidez de los ejes o los acoplamientos para desplazar la resonancia del sistema a un ancho de banda en que pueda aplicarse un método de amortiguación activa para contrarrestar las oscilaciones. Otro ejemplo es usar el análisis de frecuencias para determinar el espectro del sistema y el espectro deseado, seguido de métodos de configuración de energía. Estos métodos híbridos de tiempo y frecuencia consiguen lo mejor de ambos mundos: captar el comportamiento de las frecuencias y emplear técnicas de espacio de estados.
Turbinas eólicas
Describir las interacciones entre sistemas en una turbina eólica no siempre es fácil. La interacción aerodinámica entre el viento y las palas lleva a efectos como la cizalladura del viento y la sombra de la torre, que pueden ser percibidos como armónicos del par en el eje giratorio. Además, este último es un sistema multimasa con resonancias naturales que no se pueden ignorar. Incluso las resonancias naturales podrían contribuir a oscilaciones de par durante los transitorios.
En el otro extremo del eje, el par en el generador podría no verse libre de efecto de rizado. Dependiendo del tipo y la estructura del generador; el rizado puede tener distintos orígenes, como el dentado en generadores síncronos de imán permanente o la asimetría de tensión en la red en generadores de inducción doblemente alimentados.
Para amortiguar la oscilación torsional en estos sistemas no siempre basta el conocimiento previo de los armónicos, por lo que a veces se utiliza el análisis en tiempo real de señales medidas o estimadas (intensidad, velocidad). Pero el análisis siempre ha de ir seguido de una clasificación automática (“¿de dónde procede el armónico?”) y, por supuesto, una acción compensadora por parte del control del accionamiento. Un algoritmo típico para compensar una frecuencia simple se presenta en la figura 3.
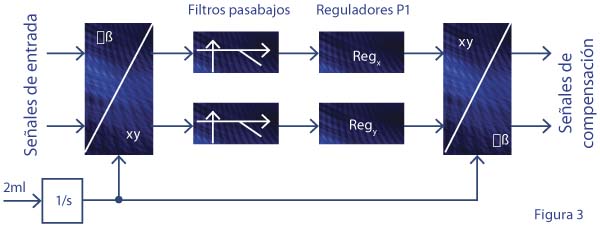
Como se ilustra en la figura 4, una emulación en laboratorio de la compensación del tercer armónico en un banco de prueba de turbina eólica a pequeña escala, donde la turbulencia emulada del viento cambia el valor medio de la velocidad mientras que el par de generación carga con la magnitud variable.
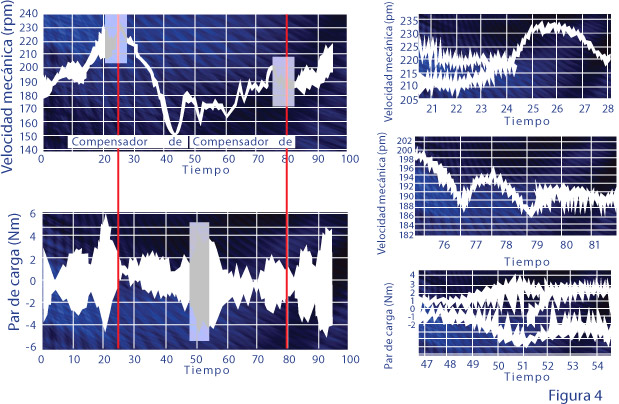
El enorme número de aplicaciones que utilizan transmisiones electromecánicas y el posible daño debido a las oscilaciones torsionales sin neutralizar obliga a prestar mucha atención a la eliminación de esos efectos perjudiciales. El diseño y las técnicas de análisis rigurosos han demostrado su efectividad.
——————————————————————————————————————————————————-
Mehmet Mercangöz
Silvia Mastellone
Stefan Almér
Thomas Besselmann
ABB Corporate Research Baden-Dattwil, Suiza
Pieder Jörg
ABB Discrete Automation and Motion, Drives and Controls Turgi, Suiza
Jouko Niiranen
ABB Discrete Automation and Motion, Drives and Controls Helsinki, Finlandia
Luca Peretti
ABB Corporate Research Vasteras, Suecia
Veli-Matti Leppänen
ABB Oy Helsinki, Finlandia




